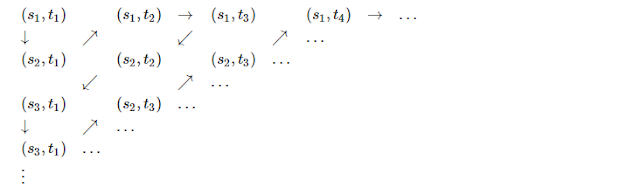Theorem
The cartesian product of two countable sets is countable.
Proof
Let k be an integer such that k>1.
Then the cartesian product of k countable sets is countable.
Let S={s0,s1,s2,…} and T={t0,t1,t2,…} be countable sets.
If both S and T are finite, the result follows immediately.
Suppose either of S or T (or both) is countably infinite.
We can write the elements of S×T in the form of an infinite table:
This table clearly contains all the elements of S×T
Now we can count the elements of S×T by processing the table diagonally.
First we pick (s0,t0).
Then we pick (s0,t1),(s1,t0). Then we pick (s0,t2),(s1,t1),(s2,t0).
We can see that all the elements of S×T will (eventually) be listed, and there is a specific number (element of N) to index each of its elements with.
Thus we have the required one-to-one correspondence between S×T and N, and our assertion is proved.
CASE - 01
Let S,T be countable sets.
From the definition of countable, there exists a injection from S to N, and similarly one from T to N.
Hence there exists an injection g from S×T to N2.
Now let us investigate the cardinality of N2.
From the Fundamental Theorem of Arithmetic, every natural number greater than 1 has a unique prime decomposition.
Thus, if a number can be written as 2n3m, it can be done thus in only one way.
So, consider the function f:N2→N defined by:
f(n,m)=2n3m.
Now suppose ∃m,n,r,s∈N such that f(n,m)=f(r,s).
Then 2n3m=2r3s so that n=r and m=s.
Thus f is an injection, whence N2 is countably infinite.
Now we see that as g and f are injective, it follows from Composite of Injections is Injection that f∘g:S×T→N is also injective.
CASE - 02
Let S,T be countable sets.
Let S={s1,s2,s3,…} and T={t1,t2,t3,…} be enumerations of S and T respectively.
Let f:S×T:N be the mapping defined as:
∀(sk,tl)∈S×T:f(sk,tl)=(k+l−1)(k+l−2)2+l+(−1)k+12k+1+(−1)k+l−12l
Then f gives an enumeration of S×T.
This enumeration can be depicted schematically as:
Hence the result.